bigger = volume or mass?
I ask kindly with a contemplative look on my face...
If you meant volume, probably correct, since that implies the diver is less streamline.
If you meant mass, probably incorrect, see below.
A neutrally buoyant diver on a reef hook would exert force based on the water that is hitting him. His mass is moot. The more streamline the diver, the less force on the D-rings.
F=ma, where:
m = mass of the water hitting the diver
a = acceleration (deceleration) of the water as it hits the diver
F = force on the D-rings.
_____________________________________________
Contrarily:
Now, if he is moving with the current, sets the hook, and comes to an immediate stop, the transient force on the d-rings is proportional to his speed and his mass. Of course, it also depends on how elastic the rope is...
F=ma, where
m = mass of the diver
a = acceleration (deceleration) of the diver
F= force on the d-rings
Since acceleration is 'change in velocity per unit time':
- Higher velocity (current) means higher acceleration, and higher force
- A more elastic rope means longer time to change speed, and lower acceleration, and lower force.
Oh, and you can always use the term 'accelerate' when talking about the physics. Deceleration is just negate acceleration.
Bigger in terms of surface area.
I'm more concerned about static force, rather than dynamic force.
I can control and minimize any dangerous dynamic force by slowly letting out the rope after I hook on, rather than letting go, flying back at the speed of the current for the length of the rope, and coming to a sudden stop.
This is a much greater force and involves computing the momentum due to the mass in motion.
p = m*v
where
p= momentum
m=mass
v= velocity
thus
F = m*a = m * (dv/dt) = (dp/dt)
knowing the diver's mass
and momentum (based on the speed of the current, length of the rope, and time from letting go of the rope, until the diver reaches the end of it and suddenly stops)
For Static Force (in the rope and on the D-Ring )...
Newton's 2nd law, as you stated it, generally applies to point masses in motion.
The case we are considering, however, is where the diver is static, and the diver/rope is opposing the force of the current on the diver, rather than that of a diver in motion.
Here we must find out how much force is exerted on the diver by the moving current.
Since the current is applying a force to the entire diver, then tension in the rope (and on the D-rings) when the diver reaches the end, due to the current is based on the surface area exposed to the current.
For example, if you drive a car at 60 mph and put your hand out of the window flat (palm facing the to the road) you do not experience the same amount of force by the oncoming air (in many cases air can be modeled as a fluid) as when you hold your hand perpendicular to the road (palm facing the wind). Yet here the the mass, the velocity, and the acceleration are the same in both cases. Only the surface area facing the wind has changed.
The formula that applies here is one that involves the mass of the moving water (density), the surface area of the diver, and the velocity of the water. Remember the diver is not moving, so his mass in not involved in this equation, per se.
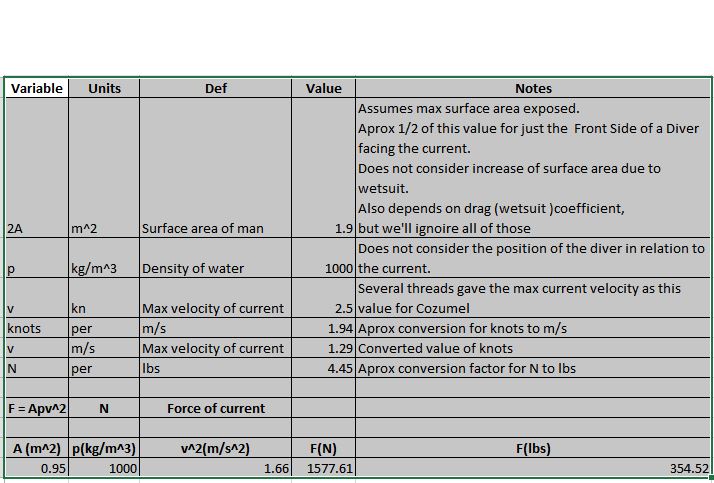
The equation needed to approximate* this force is
F= A*p*v^2
where
F = force
A=surface area of diver
p (rho) = density of water
v = velocity of water current
* for a standard man, a current of 2.5 knots, fresh water, diver facing the current with max surface area and not considering water temp, actual surface area of this particular diver based on his orientation to the current, and wetsuit/skin/etc. drag/coefficient of friction, depth, etc.
this value of force is about 350 pounds.
That is, the force on a diver hanging at the end of a rope in a 2.5 kn current is about 350 lbs.
I've attached a spreadsheet for those of you who want to check my calculations.
(It is likely I may have made a mistake somewhere, so anyone wanting to correct things, please do so.)
Here is a snapshot.
Yes, you can tell I like to play with numbers too ....