There are online calculators that will tell you your surface area. Using that you can use the thickness of the air layer around you to calculate how much lead it will take to sink that air. Every 8th of an inch is a bunch of air over the surface area of a body.Alrighty, honest question I've been scared to ask...
If you're 2 meters tall, and 100 KG, does the sheer loft of your undergarment alone play into weighting? Because (speaking from.personal experience), a 6'7", 235 lb guy in a BZ400 is kinda floaty.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Undergarment buoyancy
- Thread starter ZeroG
- Start date
Please register or login
Welcome to ScubaBoard, the world's largest scuba diving community. Registration is not required to read the forums, but we encourage you to join. Joining has its benefits and enables you to participate in the discussions.
Benefits of registering include
- Ability to post and comment on topics and discussions.
- A Free photo gallery to share your dive photos with the world.
- You can make this box go away
Why should it be different for a 2m/100kg guy compared to a 1.7m/80kg guy?
Thicker undergarments = more air in the suit = more weight
Thinner undergarments = less air in the suit = less weight
More loft in the undersuit = more air in the suit = more weight
I can't see any way that the size of the diver can eliminate those simple physical facts.
When I went from a compressed neoprene suit with only a layer or two of wool underneath to a trilam with a thick, warm undersuit, I had to add quite a few kg to my belt
Mainly because of surface area, which was/is my unsupported theory. If you laid out me and my wife's undergarments flat, mine would have something close to double the amount of material.
Basically, all those fibers are going to trap *some* air even when fully vented in normal diving conditions, and at what point does it impact buoyancy?
Like I said, not a hill I would die on, just never asked opinions on it .
TrimixToo
Contributor
Mainly because of surface area, which was/is my unsupported theory. If you laid out me and my wife's undergarments flat, mine would have something close to double the amount of material.
Basically, all those fibers are going to trap *some* air even when fully vented in normal diving conditions, and at what point does it impact buoyancy?
Like I said, not a hill I would die on, just never asked opinions on it .
Sort of an interesting question to poke at.
I found a body size to surface area calculator that says body surface area is:
BSA = SQR [BW (kg) x Ht (cm) / 3600]
So for 2m/100kg, we get a BSA of 2.36; dividing the SA by weight, we get .0236 sq cm/kg.
And for 1.7m/80kg, we get 1.9:1; dividing the SA by weight, we get .0238 sq cm/kg
So if I did the math right, the BSA does not scale linearly with size, all else being equal (but check my math). Instead, smaller people have relatively more surface area. But we have some other variables. Taller people have less surface area for the same weight. There is also body composition. Someone lean and dense will have a higher body density. The average density, from a casual Google search, appears to be .98 gm/cc, so bigger people of average density have more overall buoyancy. Undergarment fit will matter; if the fit isn't perfect (not many people match the available sizes exactly), that injects another variable. Suit fit will matter for the same reason. Inflation amount also matters, of course, which leads us to dry suit type and fit in addition to how much air is needed to stay warm in prevailing conditions.
At some point, the industry practice (estimate, test, adjust) seems simpler than trying to nail all these down. I'm sure I've missed a variable or two somewhere as well.
- Messages
- 17,327
- Reaction score
- 13,749
- # of dives
- 100 - 199
No matter whether or not your math is correct, you're right that a smaller person will have a relatively larger surface area than a large person. However, the large person will have a larger surface area in absolute numbers.if I did the math right, the BSA does not scale linearly with size, all else being equal (but check my math). Instead, smaller people have relatively more surface area.
A simple illustration: Take two identical large potatoes. They have a given surface area. Cut one of them in half. Each of the two halves will have a relatively larger (cm²/g, or in²/oz) surface area than the potato we didn't cut in half, but the intact potato will have a larger surface area than either of the two halves, in absolute numbers (cm², or in²).
TrimixToo
Contributor
No matter whether or not your math is correct, you're right that a smaller person will have a relatively larger surface area than a large person. However, the large person will have a larger surface area in absolute numbers.
A simple illustration: Take two identical large potatoes. They have a given surface area. Cut one of them in half. Each of the two halves will have a relatively larger (cm²/g, or in²/oz) surface area than the potato we didn't cut in half, but the intact potato will have a larger surface area than either of the two halves, in absolute numbers (cm², or in²).
Great illustration. The absolute surface area is only one variable, though, which is what I was trying to get at...perhaps unsuccessfully. Ultimately, it's volume and density that determine buoyancy, whether positive or negative.
So, which potato floats more in a Santi BZ400? And is it quantifiable, should someone take the time to crunch the numbers?Great illustration. The absolute surface area is only one variable, though, which is what I was trying to get at...perhaps unsuccessfully. Ultimately, it's volume and density that determine buoyancy, whether positive or negative.
This a neat little rabbit hole. Thanks gang.
TrimixToo
Contributor
So, which potato floats more in a Santi BZ400? And is it quantifiable, should someone take the time to crunch the numbers?
This a neat little rabbit hole. Thanks gang.
The Maine potato, from Aroostook County, of course. ;-)
(Naturally, I have no idea what the relative density of Maine potatoes might be compared to Idaho potatoes, but someone could do a brine float test were there enough motivation....)
In the never-ending quest to find the best undergarment, I've stumbled across the new Mares UltraSkin. Their website says it can be used with a wetsuit or drysuit. I bought a vest for use under my wetsuit on a LOB trip and it worked great. Back in the cold waters of Monterey, I tried the vest under my 300g Stretch Fleece and found it added a lot of warmth with little added buoyancy.
The UltraSkin material is quite thin compared to 300g Stretch Fleece, or my Thinsulate 400g. But still adds quite a bit warmth at depth. This got me thinking that having an undergarment that is compression resistant might mean superior performance. I decided to test all my undergarments thickness versus pressure. Keeping in mind the comments in this thread (thicker = more air = warmer = more buoyant = more diver weight to carry). But I assume not all undergarment materials are created equal, and having a thick undergarment that compresses a lot at depth is not ideal because now you're carrying the extra lead for little benefit.
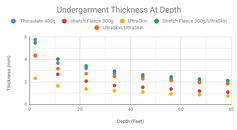
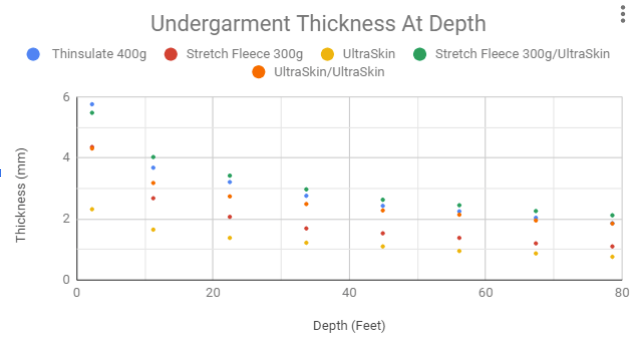
I found an apparatus that could measure thickness versus pressure (depth), and carefully measured the undergarments every 5psi. See my data below.
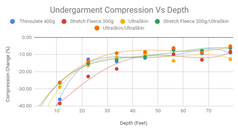
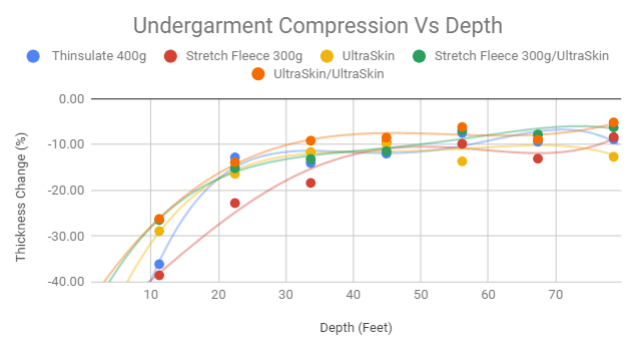
I think the better undergarment is going to be one with the higher compression resistance. This allows for less weight to carry on the surface and easier to get down that first 20feet or so. My data below shows lots of change in the first 20 feet on all the materials, with the best performer being the Mares UltraSkin, and the worst performer is the 300g Stretch Fleece. This matches my experience on ocean dives.
In the chart:
Green dots are a 300g Stretch Fleece with the Mares UltraSkin underneath (2 layers)
Orange dots are 2 layers of UltraSkin, based on the data this looks like an ideal undergarment combination.
Interesting how all the materials show lots change in the first 20 feet, and steady change after 40feet, -10% per 10 feet.
Let me know if anyone thinks I'm drawing a wrong conclusion, or if you have a superior martial (undergarment) I should test.
The UltraSkin material is quite thin compared to 300g Stretch Fleece, or my Thinsulate 400g. But still adds quite a bit warmth at depth. This got me thinking that having an undergarment that is compression resistant might mean superior performance. I decided to test all my undergarments thickness versus pressure. Keeping in mind the comments in this thread (thicker = more air = warmer = more buoyant = more diver weight to carry). But I assume not all undergarment materials are created equal, and having a thick undergarment that compresses a lot at depth is not ideal because now you're carrying the extra lead for little benefit.
I found an apparatus that could measure thickness versus pressure (depth), and carefully measured the undergarments every 5psi. See my data below.
I think the better undergarment is going to be one with the higher compression resistance. This allows for less weight to carry on the surface and easier to get down that first 20feet or so. My data below shows lots of change in the first 20 feet on all the materials, with the best performer being the Mares UltraSkin, and the worst performer is the 300g Stretch Fleece. This matches my experience on ocean dives.
In the chart:
Green dots are a 300g Stretch Fleece with the Mares UltraSkin underneath (2 layers)
Orange dots are 2 layers of UltraSkin, based on the data this looks like an ideal undergarment combination.
Interesting how all the materials show lots change in the first 20 feet, and steady change after 40feet, -10% per 10 feet.
Let me know if anyone thinks I'm drawing a wrong conclusion, or if you have a superior martial (undergarment) I should test.
Attachments
GJC
Contributor
Sort of an interesting question to poke at.
I found a body size to surface area calculator that says body surface area is:
BSA = SQR [BW (kg) x Ht (cm) / 3600]
So for 2m/100kg, we get a BSA of 2.36; dividing the SA by weight, we get .0236 sq cm/kg.
And for 1.7m/80kg, we get 1.9:1; dividing the SA by weight, we get .0238 sq cm/kg
So if I did the math right, the BSA does not scale linearly with size, all else being equal (but check my math). Instead, smaller people have relatively more surface area. But we have some other variables. Taller people have less surface area for the same weight. There is also body composition. Someone lean and dense will have a higher body density. The average density, from a casual Google search, appears to be .98 gm/cc, so bigger people of average density have more overall buoyancy. Undergarment fit will matter; if the fit isn't perfect (not many people match the available sizes exactly), that injects another variable. Suit fit will matter for the same reason. Inflation amount also matters, of course, which leads us to dry suit type and fit in addition to how much air is needed to stay warm in prevailing conditions.
At some point, the industry practice (estimate, test, adjust) seems simpler than trying to nail all these down. I'm sure I've missed a variable or two somewhere as well.
I am not understanding why you divided the body surface area by kg and how that would be useful. I think only the total BSA (not SA/kg) and thickness of insulation is useful in calculating buoyancy.
I think your assumption that bigger people have the same average body density as everyone else is flawed. Bigger people tend to have a higher fat percentage which would make them more likely to have a lower density and more buoyancy. People on Scubaboard refer to this as bioprene.
TrimixToo
Contributor
I am not understanding why you divided the body surface area by kg and how that would be useful. I think only the total BSA (not SA/kg) and thickness of insulation is useful in calculating buoyancy.
I think your assumption that bigger people have the same average body density as everyone else is flawed. Bigger people tend to have a higher fat percentage which would make them more likely to have a lower density and more buoyancy. People on Scubaboard refer to this as bioprene.
The main thing I was trying to point out was that there are a lot of variables, and "try it and see" has a greater probability of success than getting out a calculator and going diving.
The surface area of the undergarment is (more or less) proportional to BSA and to its buoyancy. SA/kg is a quick and dirty way to estimate *one* of the variables involved; one can use someone's weight to estimate BSA. I did not assume bigger people had the same average body density. You missed "There is also body composition. Someone lean and dense will have a higher body density." If you go back and read my posts above again, maybe you'll find out we agree...or maybe you'll find something I got wrong or that you disagree with, but I certainly agree that total BSA and body composition affect buoyancy already...as I wrote before.
Similar threads
- Replies
- 3
- Views
- 612
- Locked
- Replies
- 1
- Views
- 344
- Replies
- 1
- Views
- 596
- Replies
- 16
- Views
- 1,950