This might be a stupid question, but I'd rather expose my lacking understanding of physics than not learning...
I have a very simplistic understanding of the physics behind the increase in pressure as water depth increases. As I understand it, it is simply the weight of water on top you at any given depth - just like I think of atmospheric pressure as the weight of air above me at any certain place at a given time. However, given this very simplistic understanding, I'm struggling to understand why the contour of the "water container" does not affect this pressure.
Why doesn't the first shape lead to more pressure at the bottom than the second one?

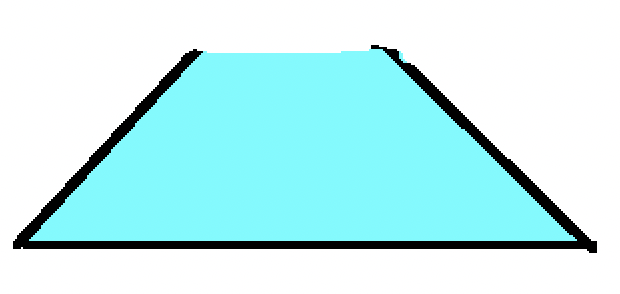
And while you are mesmerized by my mspaint skills, here comes the real reason I'm wondering:
Why is the pressure at depth in a cave the same as it would be in open water?
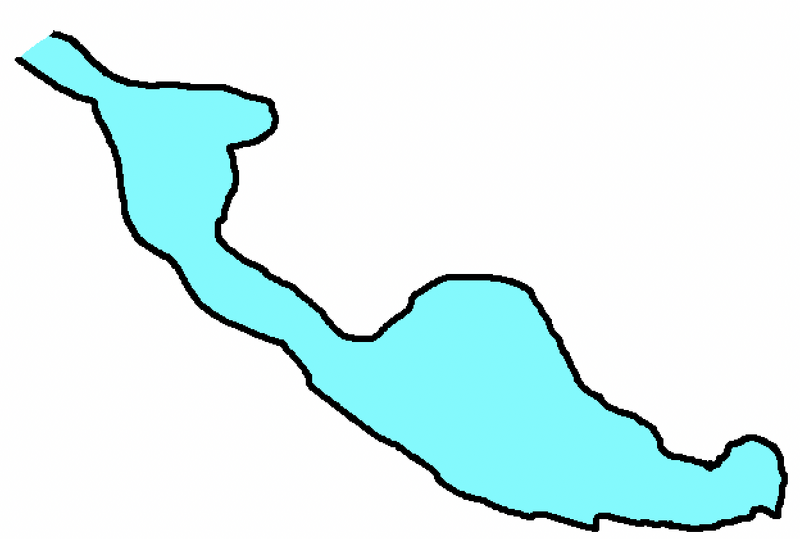
I have a very simplistic understanding of the physics behind the increase in pressure as water depth increases. As I understand it, it is simply the weight of water on top you at any given depth - just like I think of atmospheric pressure as the weight of air above me at any certain place at a given time. However, given this very simplistic understanding, I'm struggling to understand why the contour of the "water container" does not affect this pressure.
Why doesn't the first shape lead to more pressure at the bottom than the second one?
And while you are mesmerized by my mspaint skills, here comes the real reason I'm wondering:
Why is the pressure at depth in a cave the same as it would be in open water?



