marc.collin
Contributor
hi
i'm trying to convert this exemple in bar
bulhman zhl16c
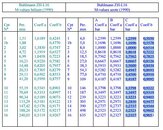
bulhman zhl16c mvalue in bar
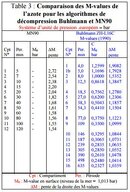
bulhman zhl16c mvalue in msw

coefficient a same to be the mvalue
if we take compartment 2
in msw we have 25,4
in bar we have 1
1 msw = 0.100693064 bar
so instead of 1 bar we shoud had 2.5576038256 bar, no?
so i tried to convert the previous example in bar
via C++ Shell i tried
i get t = 16.361300 because i used 2.55 bar instead of the 1 bar from buhlman table.
my calcul is bad or is the bulhman table who have a problem?
i'm trying to convert this exemple in bar
A diver begins an air dive by descending to a depth of 30 meters of seawater (msw)very rapidly.
Let's assume that it was an "instantaneous" descent. Now he is onthe bottom at 30 msw.
What is the "No Stop Time" or "No Decompression Limit" forthis depth?
Note: Remember all pressures are ABSOLUTE!
Assuming the dive is from sea level, the ambient pressure is the depth pressure of30 msw plus the surface barometric pressure of 10 msw:
Pamb = 30 msw + 10 msw = 40 msw
The inspired pressure is the ambient pressure minus the water vapor pressure(Buhlmann value) times the fraction of inert gas:
Pi = (Pamb - PH2O)*FN2 = (40 msw - 0.627 msw)*0.79 = 31.1 msw
The initial compartment pressure will be due to breathing atmospheric air at thesurface for a long time (first dive of the day):
Po = (Pamb - PH20)*FN2 = (10 msw - 0.627 msw)*0.79 = 7.4 msw
The surfacing M-values will vary by compartment.
See Table 2 in my"Understanding M-values" article.
Example: for Compartment No. 2 using theBuhlmann ZH-L16B M-values, Mo = 25.4 msw.
The time constant, k, for Compartment No. 2 is the natural logarithm of 2 dividedby the half-time:
k (Cpt 2) = ln2/half-time = 0.693/8 min = 0.086625
Now we can compute the "No Stop Time" or NDL for this compartment: t = (-1/k)*ln[(Pi - Mo)/(Pi - Po)] t (Cpt 2) = (-1.0/0.086625)*ln[(31.1 - 25.4)/(31.1 - 7.4)] t (Cpt 2) = 16.45 minutes
bulhman zhl16c

bulhman zhl16c mvalue in bar

bulhman zhl16c mvalue in msw

coefficient a same to be the mvalue
if we take compartment 2
in msw we have 25,4
in bar we have 1
1 msw = 0.100693064 bar
so instead of 1 bar we shoud had 2.5576038256 bar, no?
so i tried to convert the previous example in bar
via C++ Shell i tried
// Example program
#include <iostream>
#include <string>
#include <math.h>
int main()
{
float seaAtmPressure=1.00693064;
float sea30Pressure= 4.02079192;
float waterPressure = 0.0627;
float n2=0.79;
float pi = (sea30Pressure - waterPressure) *n2;
float mo=2.55;
float po=(seaAtmPressure - waterPressure) * n2;
//log(2)=0.693
//8 value of compartment 2
float k = log(2) / 8;
float t = (-1/k) * log((pi-mo)/(pi-po));
printf("k = %f\n ", k);
printf("pi = %f\n ", pi);
printf("mo = %f\n ", mo);
printf("po = %f\n ", po);
printf("t = %f\n ", t);
}
i get t = 16.361300 because i used 2.55 bar instead of the 1 bar from buhlman table.
my calcul is bad or is the bulhman table who have a problem?
Last edited: